he "Greeks" in day trading are a set of measurements used to understand the risk exposures of options positions. They are called "Greeks" because most use Greek letters as their symbols. The most commonly used Greeks are Delta, Gamma, Theta, Vega, and Rho. These measurements help traders understand how different factors affect the price of an option. Here’s how each of them is linked to price movement or momentum:
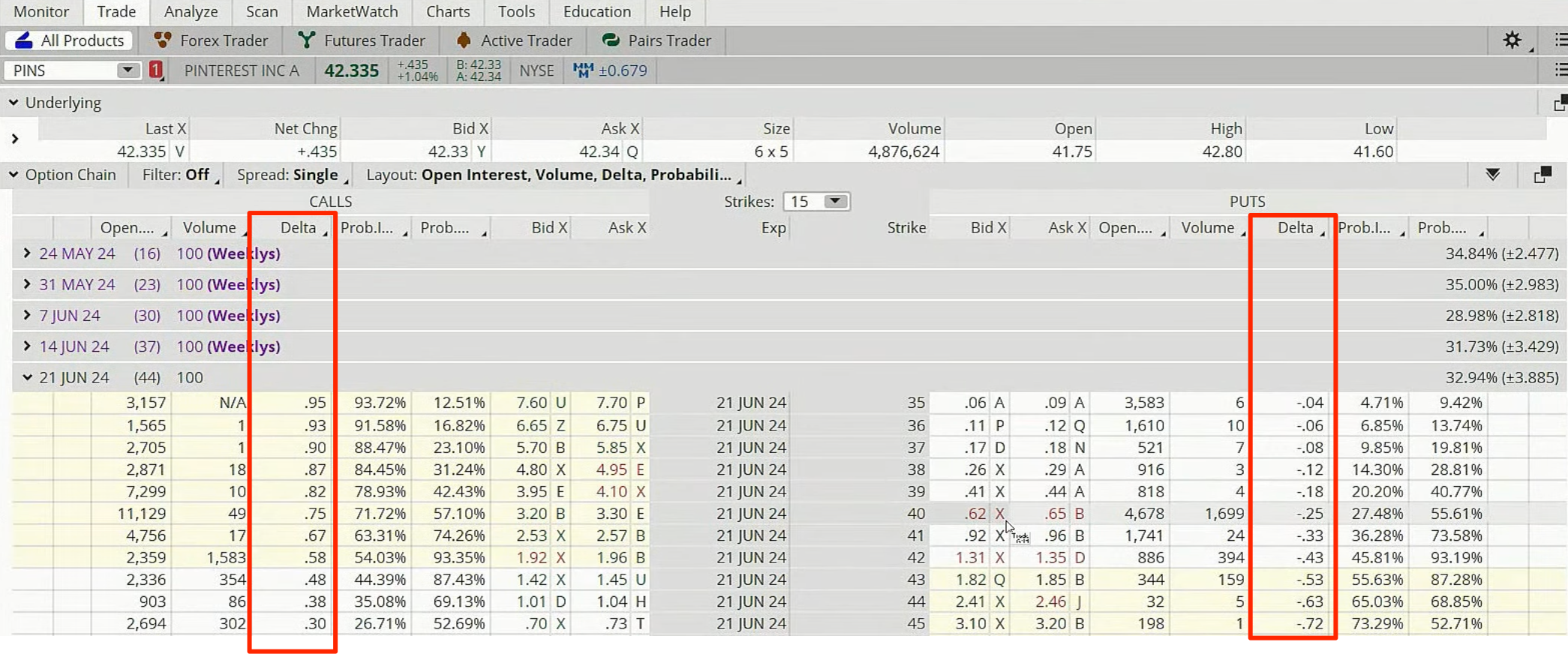
Delta (Δ)
Delta (Δ) measures how the price of an option reacts to fluctuations in the price of the underlying asset. For a $1 increase in the asset's price, Delta indicates the corresponding change in the option's price. Delta varies throughout an option's life, influenced by the asset's price and the time remaining until the option's expiry.
For put options, Delta typically ranges from zero to negative one, reflecting a decrease in value as the underlying asset's price rises. Conversely, for call options, Delta ranges from zero to one, increasing as the asset's price climbs. For instance, a call option with a Delta of .50 suggests a 50-cent change in the option's price for every $1 change in the asset's price.
Delta also serves as a rough estimate of the probability that an option will be in-the-money at expiration.
For example, take a call option with a Delta of 0.5. If the price of the underlying security increases by $2, then the price of the call option will increase by $1.
Gamma (Γ)
Gamma measures the rate of change in Delta with respect to changes in the underlying asset's price. This is important because it shows how the Delta changes as the underlying price moves. A high Gamma means that Delta can change rapidly, which can be critical for day traders in fast-moving markets. It reflects the stability of an option’s Delta and, by extension, the stability of the option’s price movement relative to the underlying asset.
Gamma is a constant measure that allows traders to estimate the likelihood of an option reaching its strike price.
Theta (Θ)
Theta measures the rate at which an option’s price decays over time, with all else being equal, particularly as the option approaches expiration. This is less critical for the price movement itself but crucial for traders to understand how time decay affects the value of their options as they hold them throughout the trading day. Sellers benefit from time decay, while buyers face increased risk as the expiration date nears.
Theta tends to become increasingly negative as it approaches the option’s expiration date.
Vega (ν)
Vega (v) measures an option's price sensitivity to changes in volatility of the underlying asset. A 1% shift in volatility can lead to a corresponding change in the option's price, as indicated by Vega. Changes in Vega reflect changes in both put and call options, with higher Vega suggesting higher sensitivity to volatility.
Rho (ρ)
Rho measures the sensitivity of an option to changes in interest rate, showing how much the price of an option would be expected to change following a 1% change in interest rates. Interest rate changes generally have a minimal impact on most options, but options with longer expiration dates are more sensitive to these changes. This sensitivity arises because interest rates represent a risk-free alternative, offering returns that could have been earned on the capital used to pay the option's initial premium.
Minor Greeks
Besides the major Greeks, there are minor Greeks that are less commonly used but still relevant:
- Lambda measures the price sensitivity of a stock to a 1% change in implied volatility.
- Epsilon gauges the sensitivity of an option's value to changes in the dividend yield of the underlying stock.
- Vomma, Vera, Speed, Zomma, Color, and Ultima assess various sensitivities related to Vega, Rho, Gamma, and changes in volatility or time.
Role of the Greeks in Options Trading
In the context of day trading, these Greeks can help traders make more informed decisions about which options to trade and how to manage their risks, particularly in relation to the price movements and momentum of the underlying securities. Understanding these metrics allows traders to predict and react to price changes more effectively, manage potential losses, and optimize the timing of their trades. They provide insights derived from mathematical formulas, typically calculated using specialized software provided by brokers.
It's important to note that options trading involves significant risk and is not suitable for all investors. Understanding and using the Greeks can help mitigate some of this risk, though they do not guarantee future performance. Investors should familiarize themselves with the risks detailed in the options disclosure document "Characteristics and Risks of Standardized Options," available through regulatory bodies or brokerage websites.












